<< Previous         Index         Next >>


Tutorial on the use of Excel for computations with the normal distributions

2. Checking normality

One way of checking is our distribution has a form similar to the normal distribution is to compute the measure of kurtosis.
To compute a measure of kurtosis we can do it with the "Kurtosis" function of Excel. We have to enter at an Excel cell the formula:
English: 
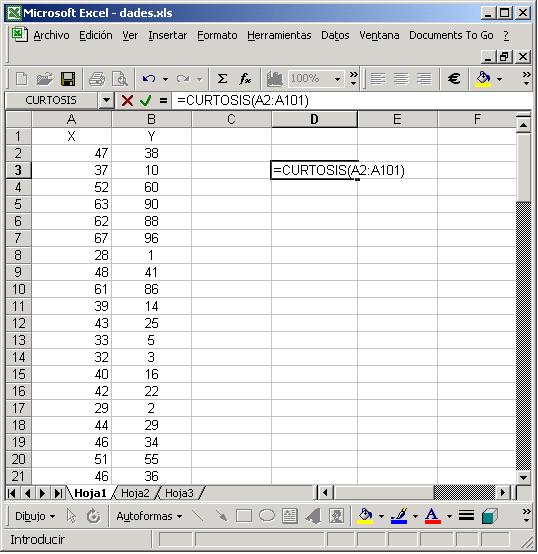
=KURT(REF1:REF2)
Spanish: 
=CURTOSIS(REF1:REF2)
Catalan: 
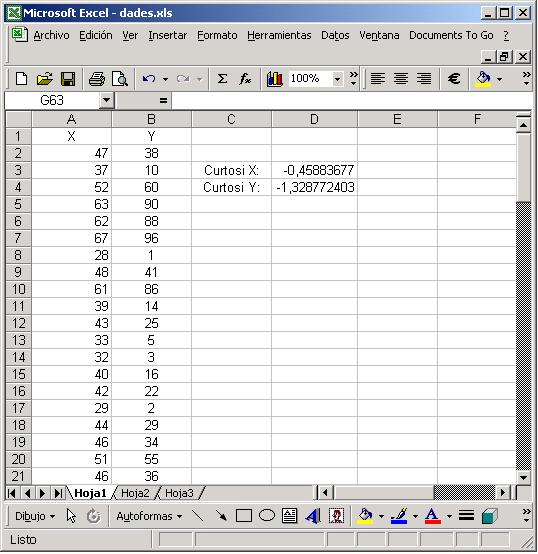
=CURTOSI(REF1:REF2)
where REF1:REF2 is a range of cells containing our data. For instance with the data that we have we compute the kurtosis of the X variable:

Here you have the kurtosis of both variables:

As you can see, the kurtosis of X is equal to −0.46 and for Y it is −1.33. How do you interpret this measure? If the distribution was exactly equal to the normal distribution the measure of kurtosis would be 0 in Excel (it would be also 0 in R, but 3 in Stata). A negative kurtosis means that your distributions is "flatter" than the normal distribution, that is the peak or modal class of the distribution is less important than the cues of the distribution, while a positive kurtosis iplies that the distribution is more "peaked" than the normal distribution. A measure of kurtosis of −0.46 is fairly small, and we cannot discard that X is normal. On the other hand note that for Y the measure is equal to −1.33, three times than the case of X and a measure that we can consider as relatively high, and this starts showing us that Y may not be normally distributed.
A part from the kurtosis, we can check the symmetry or skewness of our X and Y variables.
For instance, we can compute the mean and the median and compare them.
English: 
=AVERAEG(REF1:REF2) (català =MITJANA(REF1:REF2)
Spanish: 
=PROMEDIO(REF1:REF2) 
Catalan: 
=MITJANA(REF1:REF2) 
English 
=MEDIAN(REF1:REF2)
Catalan or Spanish: English 
=MEDIANA(REF1:REF2)
In this case:
X Y
Mean 49.59 48.58
Median 49 47
We observe that the mean of X (49,59) is very similar to its median (49), therefore the distribution is fairly symmetrical.
For the case of Y, the mean (48,58) is larger than the median (47), therefore the distribution is skewed to the right, and therefore it does not seem that the distribution can be normal (it requires symmetry).

<< Previous         Index         Next >>



File translated from TEX by TTH, version 4.08.