<< Previous         Index


Analysis of Times Series with Stata

3. Computing seasonal components and predicting with a multiplicative series

With a multiplicative series the procedures to decompose the series are very similar to the additive series. The only difference is that instead of sums and differences as in the additive series, in a multiplicative series we have to use products and divisions.
We will work with the following series:
Data for a time series
Import the data to Excel as usual. This series is quarterly, starting in the first quarter of 2016 and with 5 years of data, or 20 quarters.
We first generate the times series and we declare "Y" as a time series: 
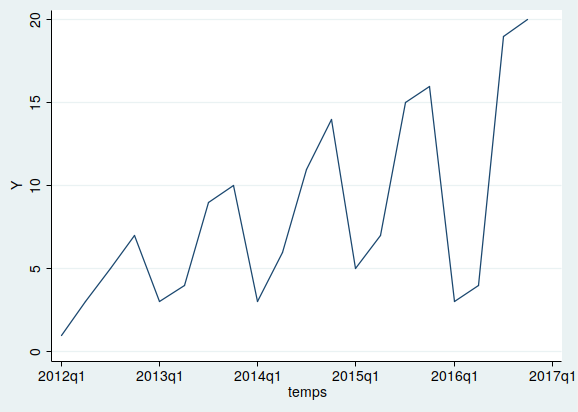
generate temps = tq(2012q1) + _n -1
format %tq temps
tsset temps
We now obtain the times series plot: 
tsline Y

As it can be seen, the series is showing an increasing trend, with strong seasonal movements that amplify over time, therefore it is appropriate to use a multiplicative model.
To obtain the centered moving averages, the procedure is the same as with the additive series. The table, once the centered moving averages of order 4 have been computed, looks as follows for this time series:

To eliminate the trend from the series we have to divide the series by the trend: 
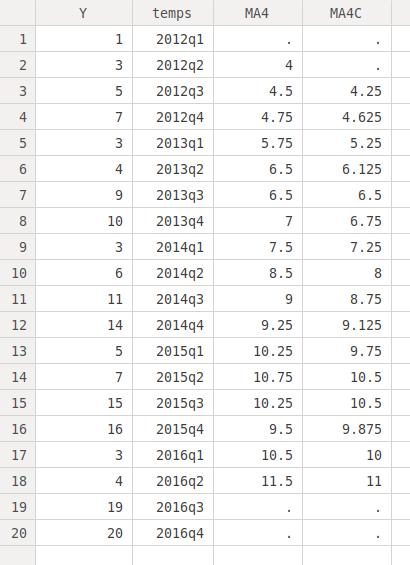
generate detrend = Y/MA4C

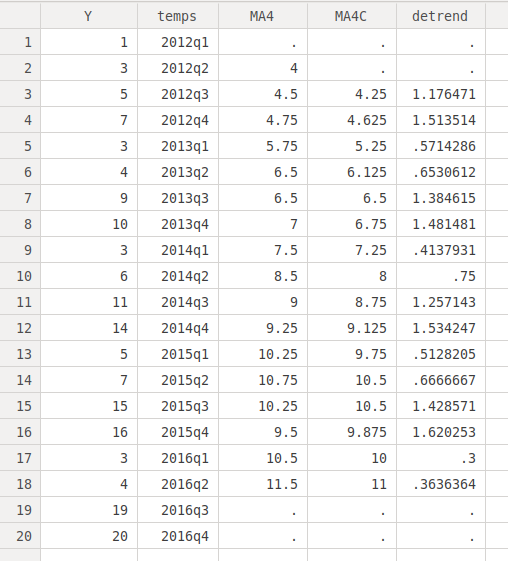
Now we do the same as in the previous example of additive series, we get the mean of the detrended series within each quarter: 
gen quarter = quarter(dofq(temps))
bysort quarter: egen season = mean(detrend)
sort temps

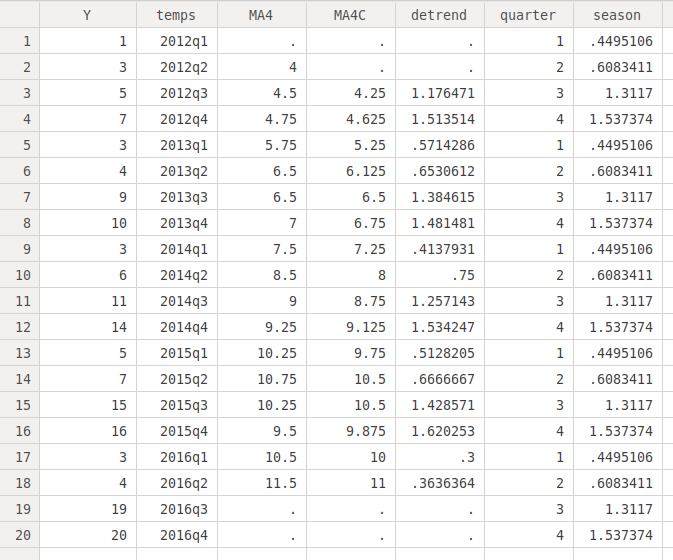
Suppose that we want to predict for the third quarter of 2017, that is three periods into the future from the last period in the series. To predict, we first get the linear trend: 
. reg Y temps

      Source |       SS       df       MS              Number of obs =      20
-------------+------------------------------           F(  1,    18) =   11.39
       Model |  244.830451     1  244.830451           Prob > F      =  0.0034
    Residual |  386.919549    18  21.4955305           R-squared     =  0.3875
-------------+------------------------------           Adj R-squared =  0.3535
       Total |      631.75    19       33.25           Root MSE      =  4.6363

------------------------------------------------------------------------------
           Y |      Coef.   Std. Err.      t    P>|t|     [95% Conf. Interval]
-------------+----------------------------------------------------------------
       temps |   .6067669   .1797891     3.37   0.003     .2290441    .9844897
       _cons |  -123.7218   39.11786    -3.16   0.005    -205.9054   -41.53823
------------------------------------------------------------------------------
And now we figure out the value of the time variable for the third quarter of 2017: 
. di tq(2017q3)
230
We now obtain the prediction for the trend for the third quarter of 2017: 
. adjust temps = 230

-----------------------------------------------------------------------------------
     Dependent variable: Y     Command: regress
 Covariate set to value: temps = 230
-----------------------------------------------------------------------------------

----------------------
      All |         xb
----------+-----------
          |    15.8346
----------------------
     Key:  xb  =  Linear Prediction
We check the value of the seasonal component for the third quarter: 
. list season if quarter == 3

     +--------+
     | season |
     |--------|
  3. | 1.3117 |
  7. | 1.3117 |
 11. | 1.3117 |
 15. | 1.3117 |
 19. | 1.3117 |
     +--------+
And we obtain the prediction adjusted by the trend, notice that we now multiply the seasonal component: 
. di 15.8346*1.3117 
20.770245
It is predicted that "Y" will have a value of 20.770245 at the third quarter of 2017.

<< Previous         Index



File translated from TEX by TTH, version 4.08.